音程をどうとるか…音階(4)
純正調だと転調できましぇん。ってどういうことか。例えばいま、ハ長調の純正調に調律されたピアノがあるとする。最も近い調であるト長調に転調してみようか。
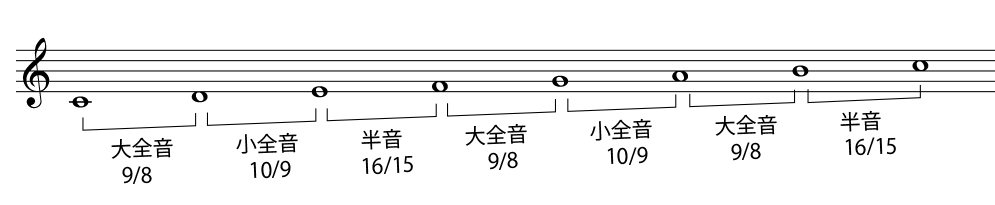
これを(ハ長調)
こうしたいわけだ(ト長調)

上の段のソ – ラと下の段のソ – ラの間隔が違う。\(\left(\displaystyle\frac{9}{8}\right)\div\left(\displaystyle\frac{10}{9}\right)=\left(\displaystyle\frac{81}{80}\right)\)だけ違う。はい、アウト!
で、平均律が登場するわけだな。ま、知っての通りオクターブ内を12に均等分割して(オクターブの振動数を12で割るという意味ではない)単位を「半音」に統一してしまえば、転調も自由だし、同一の調の中で異なる幅の3度や5度も出現しない。平均律が編み出されるまでには数多くの試行錯誤があったんだろうが、理屈はこうだ。
「音程をどうとるか…音階(1)」で書いたように、あるひとつの音から純正な完全5度を積み上げていって、12回積み上げたときにできる音\(\left(\displaystyle\frac{3}{2}\right)^{12}\)と、その音からオクターブを積み上げて7オクターブ上がったところにできる音\(\left(\displaystyle\frac{2}{1}\right)^7\)には、\[\left(\displaystyle\frac{3}{2}\right)^{12}\times\left(\displaystyle\frac{1}{2}\right)^7=\frac{531441}{524288}\]の差ができるので、この差をゼロにしてやろう、積み上げる完全5度を
\[\frac{531441}{524288}\]
の
\[\frac{1}{12}\]
ずつ狭めていってしまえば、み~んなハッピィになれるんじゃないかと。
つまりさ、オクターブの次に協和する完全5度に「手を付けちゃった」わけよ。凄いことだよ。後の西洋音楽の和音和声による発展で私達が得たものの大きさを考えると、この「完全5度に手を付けた」「大胆な合理化」「妥協した」・・・なんと言っても良いが、そしてこれを誰かが決断したものでもないだろうが、この決断は恐ろしいほど偉大だ。「完全さの追求」や「真実の探求」とは 真逆の方向へ進んだのだから。な、いつも言ってるだろ、「正しく演奏しようとするな!」って。
で、人間の耳って一体どうなってるんだろうって。片や旋律の追求をすると11や13や17の素数をもってしか分割できないような音程を求めるのに、一方では狂った完全5度でも「わぁ、きれい!」なんて言ってんだから。我々の耳は、繊細で、精密で、大胆で、いい加減なんだね。それは別の言い方をすれば、計算で聴いているわけではないし、計測器のように聴いているわけでもない。我々は生きていて、聴覚も生きている。生きるってそういうもんよ。繊細でいて、いい加減なんだよ。わたしたちは生きていて、故にそれを感じている、と言うしかない。
きょうはここまでだ。きゅうりの苗が萎れてる。
コメントを書く