音程をどうとるか…音階(3)
昨日までの話で足りない部分を補足しておこう。まず、短調についてだ。前回、音階を形成するために、主音、その5度上の属音、主音の5度下の下属音の上に、「長3度と短3度によって分割された3和音を構成する。」と書いたが、この3度の順を下が長3度、上が短3度で構成すると「長音階」であり、下が短3度、上が長3度で構成すると「短音階」になる。

長音階
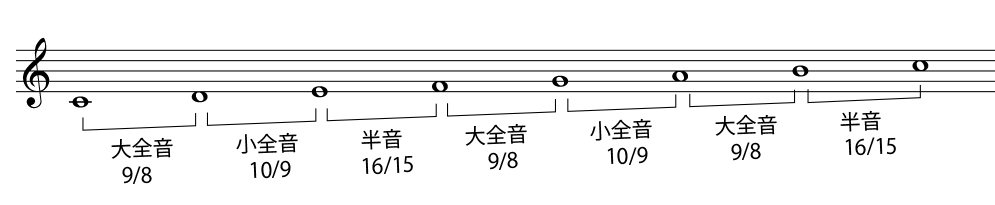

短音階

そして、オクターブを分割するうえで何故2,3,5の素数で分割が終えられたのか。これは、これらの音階が、和声和声的に西洋音楽を分析するうえでこれ以上の細分化の必要がないからだ。単純な比で表される音程ほどよく協和するという原則があるからだ。ただし、その音楽、退屈!(3)で少しだけ触れた第7倍音(自然7度)は、ナチュラルホルンではよく用いられる音で、その上の主音との振動比は8:7である。記譜上は上記短音階の第7番目の音と同じなのだが、当然それよりはかなり低い。ついでながら行っておくが、この美しく響く自然7度は「純正律」ではない。そして、西洋音楽から音楽の範疇を世界へ拡げていけば、民族によっては7を用いた分割は非常によく現れ、あるいは11、13,17までも用いる民族もあったという。繰り返すが、これらの音程は、「和音」を基礎として発展した西洋音楽においては邪魔者でしかないのである。別の言い方をすれば、旋律線の追求によって音楽を追求した民族は、より高度な音程差を獲得することが出来たが、音を重ねることに価値を見出した民族=西洋は高次な素数によるオクターブの分割を早々と放棄した代わりに、和声というとてつもない財産を手にすることが出来た、といえる。
しかし、このとてつもない財産を手に入れるまでには、まだまだ苦労しなければならないのだ。上記の長音階において、

の部分に注目しよう。この音程差は\(\left(\displaystyle\frac{10}{9}\right)\times\left(\displaystyle\frac{16}{15}\right)\times\left(\displaystyle\frac{9}{8}\right)\times\left(\displaystyle\frac{10}{9}\right)=\left(\displaystyle\frac{40}{27}\right)\)
となる。あちゃぁ~、完全5度じゃないやん。完全5度は\(\left(\displaystyle\frac{3}{2}\right)\)だから、\(\left(\displaystyle\frac{3}{2}\right)\div\left(\displaystyle\frac{40}{27}\right)=\left(\displaystyle\frac{81}{80}\right)\)となって\(\left(\displaystyle\frac{81}{80}\right)\)だけ低くなってしまう。この例にとどまらず、純粋に調和するであろう純正律という音階の中には、やや高めの完全4度や、やや低めの短3度が存在してしまう。その事によってまず真っ先に起こる不都合が「転調できましぇん」問題である。
話が佳境に入ってきたぞ。いよいよ次回はみんな大好き平均律の話だ。ヒントだけ出しておこうかな。
「フルートは鍵盤楽器じゃない」
きょうはここまでだ。読むのはキツイだろうが、書いてる俺もキツイんだ。
コメントを書く