音程をどうとるか…音階(2)
前回は、物理的に「協和」させるための振動数の分割について述べた。ここでいう「協和」とは協和音という意味ではなく、最も協和するオクターブから始まってその内部をできるだけ単純な比で分割していく様を順に並べただけだ。その条件はこうだ。
1)\(\left(\displaystyle\frac{n+1}{n}\right)\)で分割する。(nは整数)
2)使用する整数は2、3、5、によって構成される。
この条件によって導き出された音程は、
完全5度+完全4度
長3度+短3度
大全音+小全音
大半音+小半音
の8つの音程だった。これ以上は無い、また完全4度を\(\left(\displaystyle\frac{n+1}{n}\right)\)で分割するには7の助けを借りなければならない。\(\left(\displaystyle\frac{7}{6}\right)\times\left(\displaystyle\frac{8}{7}\right)=\left(\displaystyle\frac{4}{3}\right)\)
この段階ではまだ「音階」を構成するには至らない。音階を構成するために次のように考える。ある音を中心に(主音)その完全5度上(属音と呼ぶ)と完全5度下(下属音と呼ぶ)に長3度と短3度によって分割された3和音を構成する。主音をC(ド)としたものを譜例で示す。

ここで得られた音を1オクターブ内に再配置すると、
次のように7つの音が得られて音階が成立する。

ああ良かった。😊 でも、安心するのはまだ早いぜ。各音の音程はどうなっているのか、短調もあるしな。とりあえず、各音程を調べてみよう。細けぇ計算は省略な。数式書くのすげぇ面倒だから。
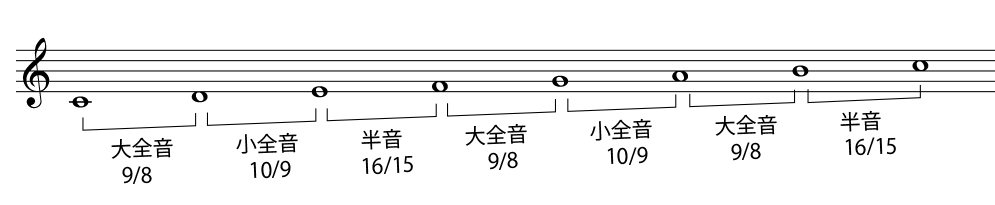
おお、だいぶスッキリしてきたな。半音は16:15の大半音一種類に収まったみたいだな。全音に2種類あるのが気に食わん人も居るだろうが、そういう人は頭が平均律に毒されたと思ったほうがよろし。これが純正律だ。
「おお、そうか、そういう風に吹けばいいんだな。」と思った人、それ違うから。
「これと平均律との差をチューナーで補正してやればいいわけだ。」と思った人。それもっと違うから。
では、なぜこんな面倒な話をしているかと言うと、これらの理屈が「演奏に役立ったためしがない」からで、理論があって音楽ができたのではなく、苦労に苦労を重ねてようやく実践された音楽が理論的に分析されたに過ぎないからだ。その苦労の末に得たものは、音楽の偉大な発展であり、失ったものは我々の聴覚だと言える。なんだか結論めいたことを書いてしまったが、七面倒臭い話はもっと続く。お願いだから、もう少し我慢して読み続けてくれ。ここでこう書いておかないと、面倒な話はイヤよって逃げられちゃうし、おいらがゴリゴリの理論派だと思われても迷惑だからな。最後に大どんでん返しがあるよ。
きょうはここまでだ。眠い。譜例の楽譜を造るのも結構大変なんだよ。
コメントを書く